ESPNLocal NetworksBy Matt Clapp on

During Monday night’s game between the Pittsburgh Steelers and New York Giants, Dan McNeil of Chicago’s 670 The Score sent out the following tweet about ESPN sideline reporter Maria Taylor: “NFL sideline reporter or a host for the AVN annual awards presentation?”

Yikes. The tweet was up for nearly 30 minutes, before McNeil finally deleted it (after he likely received several requests to do so).

McNeil co-hosts the McNeil & Parkins Show, which has the 2-6 p.m. CT weekday slot on WSCR-AM 670. He has been in Chicago sports radio for more than 30 years.

McNeil’s tweet comes after 670 The Score’s Bruce Levine tweeted a photoshopped political and vulgar image on Aug. 23, before deleting it and apologizing in a follow-up tweet. Levine was back on the air a week later, but has been silent on Twitter since the apology tweet.

In 2010, ESPN suspended Tony Kornheiser for two weeks after he said that Hannah Storm was in a “horrifying, horrifying outfit.”

UPDATE: Upon learning of McNeil’s remarks, several of Taylor’s colleagues responded. Taylor herself even tweeted a rebuttal.

https://twitter.com/elleduncanESPN/status/1305702987302608897

UPDATE: McNeil has been fired by The Score.

https://twitter.com/JulieDiCaro/status/1305934434806439938

88 thoughts on “Chicago radio host Dan McNeil suggests Maria Taylor’s outfit appropriate for adult film awards show (UPDATE: he’s been fired)”

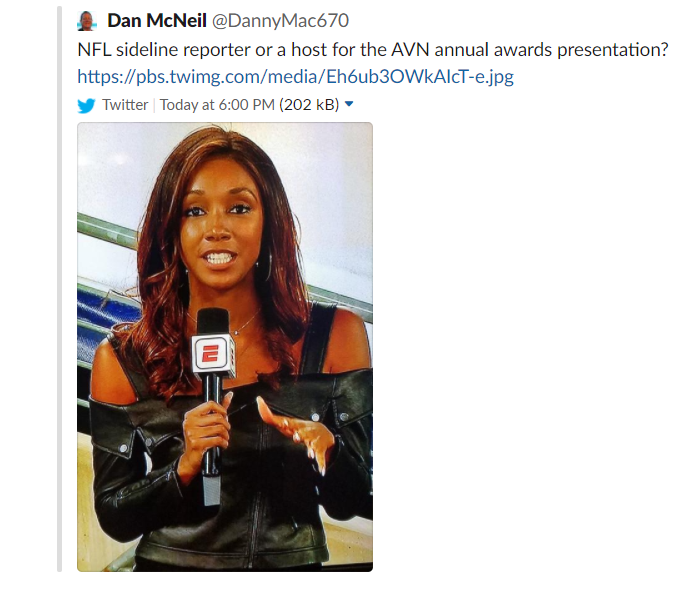
  1. Dan McNeil , the quintessential sports talk show gas bag….Time spent listening to him are moments out of your life you can never get back….Need I say more ?

  3. I’m sure you mean that to be insulting to women, but what you really just said is men can’t control themselves it’s not our fault. Think about that for a while.

      1. Do you not know how these work?
        It was a response to a comment.
        Maybe you should ask your question of yourself.

      3. I don’t know,
        are you actually using a term for a disability, as an insult ?
        you need to jump in a Petri dish and finish evolving.

  5. She looked fine and would have with anything on or off! Dan McNeil would only look good with a Bag over his face!

    1. Well…a man’s face isn’t women’s favorite part of their body anyway. And Dan looks good for his age. Are you blind?

  6. Comical. Eat a few cookies or something. What little body she has couldn’t come anywhere close to making that outfit work.

    1. Just because you’re grossly obese doesn’t make it an attractive look.

  7. First of all when did it become a man’s place to tell a woman what she can wear and can’t wear. He has a face no one wants to see but on a radio

    1. It was a tweet, dumbass. Nobody is forcing anybody into anything. Read the fucking article.

      1. Try to refrain, Ben, from using the Democrat words here in public.

      2. you sound like the typical white male that sexually frustrated, you can’t tell anyone what they can are can’t do. I’ll leave the name calling to you

  8. We live in a society now where nothing women do or say can be criticized no matter how justified. Look at how many women have taken mens jobs in sports reporting just because they are pretty.

    1. SInce when is a job classified only as a “man’s job.” What decade do you live in? The 1940’s or 50’s and your parents were Ward and June Cleaver and you went to the family Doctor, Doctor Marcus Welby. Times have changed and that’s good. Get with it.

      1. You get with it yourself. I’m actually lucky I’ll be dying soon enough and people like you can fester in this awful world you are creating for the future. I’m glad I won’t be here to see it. It’s all downhill from here with thinking like yours.

        3. Treating women with dignity? Giving them equal opportunity in employment? Not attacking a woman’s looks or sexuality anytime that someone is threatened by them? That’s an awful world? I know in your generation sexism and racism was acceptable and Trump made you feel like it is okay again – but it is definitely not. You are a hateful ignorant relic and you will be remembered as such.

          Thanks for leaving a polluted world that is becoming inhospitable for future generations. It is going to take multiple generations to reverse the damage yours did. We will not be forgetting that either.

          1. I can certainly agree with that.
            really love the people that want to paint people as some sort of radical liberal or socialist if you actually think about the bigger picture and others rather than everything in life just being about yourself, and you not agreeing with the way they see things.
            it’s good to see it’s on its way out.
            I’m 58 years old and I’ve never treated anybody or anything that way.
            and have always pretty much despised people that do.
            Trump is hopefully going to be the last sickening example of that kind of selfish, destructive, ignorant/ ugly thinking…
            USMAELS sorry your life is ending and that you’re leaving it with such shitty thoughts.

      2. No, that is not so “good.” Time has produced poges like you. That is bad.

        1. Thanks for announcing your developmental disorder to the world.

    4. Maybe if you actually criticized them instead of just ranting like a sexist idiot, you wouldn’t have this problem.

    5. “taking men’s jobs.”
      that is so ignorant on so many levels I don’t even know where to begin…

  9. Was she screaming about white privilege like that other racist gas bag Stephen A. Smith? BSPN is just the epitome of irony considering the SEC and the political audience it caters to. The double standards will never end in this country.

    1. Ahahahaha found the pathetic loser who can’t stand variety. You call it BSPN and then complain about THEM making it political? Good job on being a failure.

  11. It was pretty funny while reading this article there was a sexy girl on an ad from a popular adult toy store on the same page. Probably because we by from them. There’s no prude in our marriage…my wife finds joy in looking like a milf. She’s in her sixties, and she’s been mine for almost 40 years. I’m lucky man.

  12. He basically called her a milf, and she probably hoped she looks the part and is happy he noticed. Along with all the other men and women who also thought he analogy was right on. I’m still having sweet thoughts about her…he was right…she’s gorgeous. What? I mean…does anyone believe we want to see some girl that resembles Nancy Pelosi instead. Yuk.

  14. Did anybody actually read the tweet, instead of the misleading headline? Bunch of retards in here happy to cancel somoneover a joke.

    1. why are you so tight dude and what with the name calling, you sound like another sexually frustrated white male. let a women wear whatever the hell she wants it’s none of your business.

    2. Dude you cancel yourself when you make dumb-ass comment, you sound like a trump fan boy

  15. It’s too bad we can’t see her underwear. That would probably prove his point, lol!Then we could tell if he was right or not. Especially if she’s not wearing any. Place your best. I say she at least had a hot looking g string. I also bet thet both fantasized about each other later. Come on people…old guys need love too. Like we all want to see plain dressed ladies looking frumpy instead.

    1. You shouldn’t have elected to get that lobotomy. It’s clearly made you retarded.

    1. no it was the worst and only non existant, made up, fantasy point.

  18. You obviously haven’t seen club attire lately that was not close.If she was a white woman showing a little cleavage I wonder if he would’ve accepted that and just thought of her as an attractive woman? I’m sorry but it’s something especially nowadays about dark skin people.Its the us and them syndrome these days.smh

  19. Not a fan of her outfit, dudes statement was harsh though…

  20. You are right. As the only female on an all male team in IT, dressing appropriate is how I got respect in the beginning- b4 my skill set took over

  21. “or working a corner after the game”

    Know how I know you’re a basement dweller?

  22. I thought she was rocking it. Looking like she was ready to go see Judas Priest do a gig. He is just jealous he can only wear something like that in the privacy of his bathroom looking at himself in the mirror while listening to White Horses!

  23. her dressing “appropriately” or not is something up for debate. whether his reference to it was completely out of line/ignorant and not something you should say, isn’t.

  25. Does she understand the game? Add any value to the telecast? If so good. If not then show somebody who does.

  26. There always has to be someone to toot the black/ white horn. Whether black, white, or whatever color, your a sideline football game reporter; there to report not distract or draw attention to yourself. Dress appropriately. And as for the horn tooter; GET A LIFE!

    1. Looks appropriately dressed to me and anyone else not living on the Puritan commune.

    2. Looks appropriately dressed to me and anyone else not living on the Puritan commune.

  27. The man’s comments were off the wall by the way. But there’s a difference between sexist and racist. Jeeze!

  28. Hmmmm it can go both ways…looking at his picture….low-rent sports announcer or middle-school principal-looking doofus that can’t get laid?????

  29. I’ve seen other reporters wear WAY LESS than that and he didn’t say shit, so why now?

  30. That outfit is a bit weird for working a game but whatever. Maria Taylor is gorgeous, I don’t really care how she dresses.

  31. What the hell is wrong with everyone, free to say what you feel, but everyone gets their feelings hurt over anything you say, a bunch of damn crybabies everywhere you look. Talk about a oppressive society…You cant even talk to people without worrying they take something the wrong way and start tattle telling. You can’t even talk to women without fear of them taking something and twisting it. Seems as if everyone are raising punks & sissies, who have thin skin. WOMEN everywhere are screwing everything up with their crappy hypocrite ways. We want equality, but we want to be treated differently….MAKE UP YOUR DAMN BIPOLAR MINDS!!

    1. And here you are, crying like a crybaby. Can’t even make this up…

  33. Maria had 1,729 kills playing volleyball at the Univ of GA. Let’s put Dan one side of the net with a setter and Maria of the other side of the net with a setter and let them play some ”friendly” rallies . They can announce the number of Molten sandwiches Dan consumed in 10 minutes (if he lasts that long) on SportsCenter.

  34. I’m quite sure she took it as a compliment. Thankfully, most women today STILL enjoy flirtatious comments and realize they are compliments, especially when the ladies are dressed cute and certainly hope men notice. If anyone doubts she actually loved the funny compliment from him, then they simply don’t understand that women are as sexual as men. Now days especially…and good for them. It’s what makes the world go round. I’m pretty old…at least according to my kids…and I assure you many many women would be flattered by his complimented. Girls just like to have fun…doesn’t anyone remember that anymore? Obviously he found her attractive, and she definitely was dressed in a way to look that way. There’s no story hear, except for man haters. There’s no shortage of them now days either. Anyone that goes out on the town now days realizes that often when you see a group of the cutest and sexiest girls…there’s a decent chance they don’t like men and prefer men. Fact. That said, there’s thankfully plenty of women who indeed still like flirting it up with the boys. I actually detected some chemistry between them, lol….it wouldn’t surprise me if they hooked up sooner or later. She definitely knows he’d be interested. What guy would not…she is a living doll…and that is all he meant. She probably loved his remark.

  35. She was dressed EXACTLY like the female prostitutes in our city. But, hey, it is the NFL, and that is also exactly like the red light district of our city.

  36. Sure buddy, im sure that’s exactly what it is and not contracts that actually do not apply to freelance reporting.

  38. These people always do these things, then say Sorry. REALLY????? Deep down they know who they are towards Women with out regards then???? ?? They don’t do this to their Sisters??? ??

Comments are closed.

About Matt Clapp

Matt is an editor at The Comeback. He attended Colorado State University, wishes he was Saved by the Bell's Zack Morris, and idolizes Larry David. And loves pizza and dogs because obviously.

He can be followed on Twitter at @Matt2Clapp (also @TheBlogfines for Cubs/MLB tweets and @DaBearNecess for Bears/NFL tweets), and can be reached by email at mclapp@thecomeback.com.

View all posts by Matt Clapp